Un solide tronqué est un solide qui a été coupé par un plan et dont seulement une portion de la séparation a été conservée. Ce plan de coupe peut être parallèle à la base de ce dernier ou non.
Il est important de savoir qu’on peut tronquer n’importe quel solide. Dans certains cas, le solide obtenu est similaire au solide initial et on peut calculer son volume facilement. Par contre, dans le cas des pyramides et des cônes tronqués, il faut utiliser une démarche différente en se servant de la soustraction. Voici 2 exemples.
Pour isoler le toit d'une maison, un entrepreneur décide d'utiliser une mousse de polyuréthane appliquée à l'aide d'un pistolet. Une fois la mousse durcie, elle aura l'allure d'une pyramide tronquée à base rectangulaire.
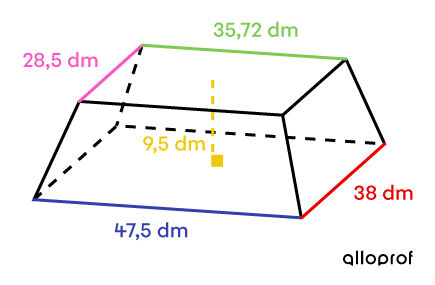
Si ce produit coute |4\ $| pour |9\ \text{dm}^3,| quelle somme d’argent sera nécessaire pour isoler ce toit?
-
Identifier les solides
Dans le cas présent, il s'agit d'une pyramide tronquée à base rectangulaire. Dans le but de faciliter les calculs, on doit retrouver la pyramide initiale associée à celle qui est tronquée pour ensuite en déduire ses dimensions comme ceci :
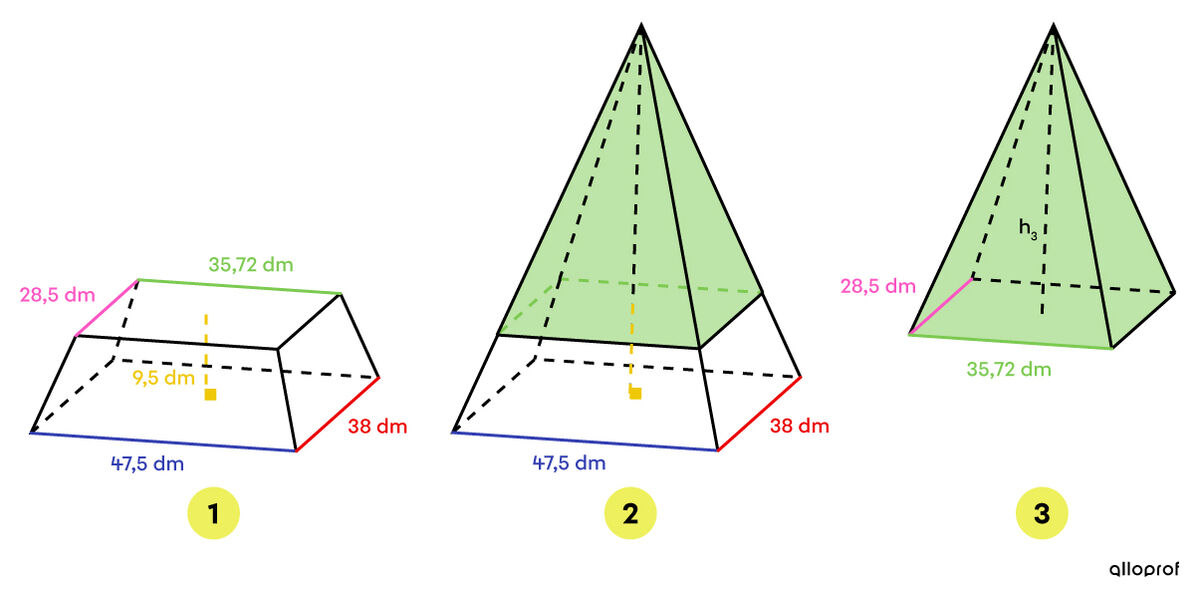
Dans une pyramide tronquée comme dans un cône tronqué, les mesures homologues sont proportionnelles.||\dfrac{\text{Longueur}_2}{\text{Longueur}_3} = \dfrac{\text{largeur}_2}{\text{largeur}_3} = \dfrac{\text{hauteur}_2}{\text{hauteur}_3}||Pour calculer la hauteur de la pyramide qui est enlevée (la pyramide 3), il faut donc résoudre une proportion.||\begin{align} \dfrac{\color{#EC0000}{\text{largeur}_2}}{\color{#FF55C3}{\text{largeur}_3}} &= \dfrac{\text{hauteur}_2}{\text{hauteur}_3} \\\\ \dfrac{\color{#EC0000}{38}}{\color{#FF55C3}{28{,}5}} &= \dfrac{h_3+\color{#EFC807}{9{,}5}}{h_3} \\\\ 38h_3 &= 28{,}5(h_3+9{,}5) \\ 38h_3 &= 28{,}5h_3 + 270{,}75 \\ 9{,}5h_3 &= 270{,}75 \\ h_3 &= 28{,}5\ \text{dm} \end{align}||On peut en déduire la hauteur de la pyramide complète (la pyramide 2).||\begin{align} h_2 &= h_3 +\color{#EFC807}{9{,}5} \\ &= 28{,}5 + \color{#EFC807}{9{,}5} \\ &= 38 \ \text{dm} \end{align}||
-
Calculer le volume
Le volume du toit (image 1) est obtenu en soustrayant le volume des pyramides 2 et 3.||\begin{align} V_{1} &= V_{2} - V_{3}\\ &= \dfrac{A_{\text{base}_2}\times h_2}{3} - \dfrac{A_{\text{base}_{3}}\times h_3}{3} \\ &= \dfrac{(47{,}5 \times 38) \times 38}{3} - \dfrac{(35{,}72 \times 28{,}5)\times 28{,}5}{3} \\ &= \dfrac{1 \ 805 \times 38}{3} - \frac{1 \ 018{,}02 \times 28{,}5}{3} \\ &\approx 22\ 863{,}33 - 9 \ 671{,}19 \\ &\approx 13 \ 192{,}14 \ \text{dm}^3 \end{align}|| -
Interpréter la réponse
On peut établir une proportion et la résoudre en utilisant le produit croisé. ||\begin{align}\dfrac{4\ \$}{?} &= \dfrac{9 \ \text{dm}^3}{13 \ 192{,}14\ \text{dm}^3} \\\\ ? &= \dfrac{4 \times 13 \ 192{,}14}{9} \\ ? &\approx 5 \ 863{,}17\ \$ \end{align}||Ainsi, l'isolation avec cette mousse coutera environ |5\ 863{,}17\ \$.|
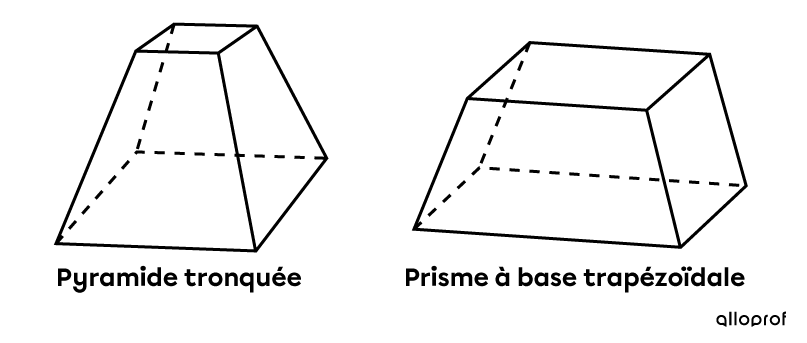
Dans ces situations, il faut faire attention de ne pas confondre une pyramide tronquée avec un prisme à base trapézoïdale. Dans le cas de la pyramide tronquée, les faces latérales sont des trapèzes inclinés vers l'intérieur du solide, alors que dans le cas du prisme, les bases sont des trapèzes isométriques et les faces latérales sont des rectangles.
Pour avoir une belle récolte de légumes, une horticultrice plante des graines de tomate dans des pots en forme de cône tronqué inversé.
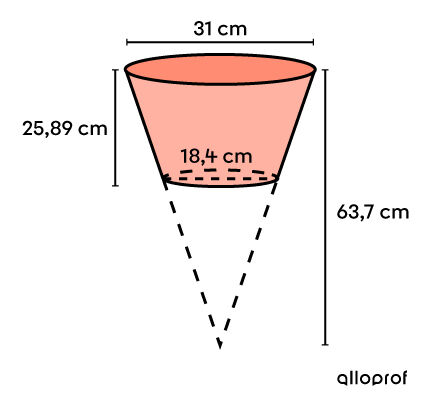
Pour produire suffisamment de tomates, elle doit avoir 14 plants. Sachant qu’elle remplit ses pots à pleine capacité, de quelle quantité de terre aura-t-elle besoin pour planter toutes les graines?
-
Identifier les solides
Dans le cas présent, il s'agit d'un cône tronqué inversé. Dans le but de faciliter les calculs, il est important de considérer le cône initial.
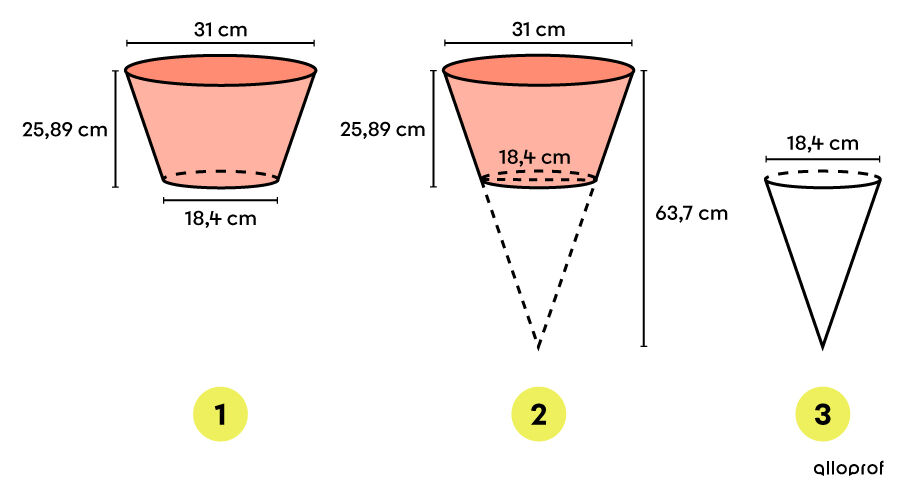
-
Calculer le volume
Le volume du pot (image 1) est obtenu en soustrayant le volume des cônes 2 et 3. ||\begin{align} V_{1} &= V_{2} - V_{3}\\ &= \frac{A_{\text{base}_2}\times h_2}{3} - \frac{A_{\text{base}_{3}}\times h_3}{3}\end{align}||Comme il s’agit de cônes, la base est un disque. Ainsi, on utilisera la formule suivante :||A_{\text{base}} =\pi r^2||Il faut trouver les rayons puisque ce sont les diamètres qui sont donnés. ||r_2 = \dfrac{31}{2} =15{,}5\ \text{cm}\\r_3 = \dfrac{18{,}4}{2} =9{,}2\ \text{cm}||Il faut aussi calculer la hauteur du cône 3. ||h_3 = 63{,}7 - 25{,}89 = 37{,}81\ \text{cm}|| ||\begin{align} V_{1} &= V_{2} - V_{3}\\ &= \dfrac{A_{\text{base}_2}\times h_2}{3} - \dfrac{A_{\text{base}_{3}}\times h_3}{3} \\ &= \dfrac{(\pi \times 15{,}5^2) \times 63{,}7}{3} - \dfrac{(\pi \times 9{,}2^2)\times 37{,}81}{3} \\ &= \dfrac{240{,}25\pi \times 63{,}7}{3} - \dfrac{84{,}64\pi \times 37{,}81}{3} \\ &\approx 16\ 026{,}23 - 3 \ 351{,}28 \\ &\approx 12\ 674{,}95 \ \text{cm}^3 \end{align}|| -
Interpréter la réponse
Le volume de terre trouvé est pour 1 pot. Comme il y en a 14 à remplir, on fait le calcul suivant : ||14\ \text{pots} \times 12 \ 674{,}95\ \text{cm}^3/\text{pot}=177 \ 449{,}3 \ \text{cm}^3||Ainsi, la quantité de terre nécessaire est d’environ |177 \ 449{,}3\ \text{cm}^3.|
Il est possible d’utiliser des formules plutôt que d’appliquer les démarches précédentes. Par contre, les formules sont différentes selon la nature du solide tronqué.
-
Le volume d'un cône tronqué
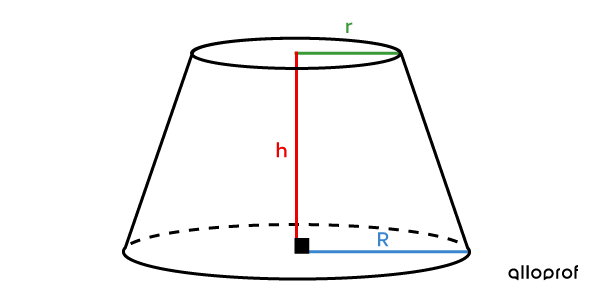
||V = \dfrac{\pi\color{#ec0000}{h}}{3}\Big(\color{#3B87CD}{R}^2+ \color{#3B87CD}{R} \color{#3A9A38}{r} + \color{#3A9A38}{r}^2 \Big)\\ \text{où}\\ \begin{align} \color{#ec0000}{h} &: \text{hauteur du cône tronqué} \\ \color{#3a9a38}{r} &: \text{rayon de la petite base} \\ \color{#3B87CD}{R} &: \text{Rayon de la grande base} \end{align}||
-
Le volume d'une pyramide régulière tronquée
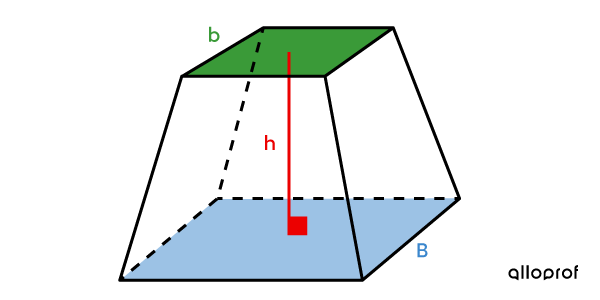
||V = \dfrac{\color{#ec0000}{h}}{3}\Big(\color{#3B87CD}{B} + \sqrt{\color{#3B87CD}{B}\times \color{#3a9a38}{b}}+ \color{#3a9a38}{b} \Big)\\\text{où}\\\begin{align} \color{#ec0000}{h} &: \text{hauteur de la pyramide tronquée} \\ \color{#3a9a38}{b} &: \text{Aire de la petite base} \\ \color{#3B87CD}{B} &: \text{Aire de la grande base} \end{align}||
Malgré ces dernières formules, les démarches présentées dans les exemples s'avèrent plus efficaces puisqu'on peut les réutiliser lorsqu’on cherche une mesure manquante dans ce genre de solide.